一周技术博客收集-20220606
Java HashMap的死循环
[1.7版本的java,1.8已解决这个问题,但是hashmap在多线程下依然可能出现别的问题]介绍了hashmap在多线程下可能出现的问题,可以深入了解为什么hashmap是线程不安全的。
New language features since Java 8 to 18
介绍了java8-18的新特性。
Java锁与线程的那些事
一篇很详尽的介绍java锁的文章
MySQL之Binlog
简单了解下Binlog
[1.7版本的java,1.8已解决这个问题,但是hashmap在多线程下依然可能出现别的问题]介绍了hashmap在多线程下可能出现的问题,可以深入了解为什么hashmap是线程不安全的。
介绍了java8-18的新特性。
一篇很详尽的介绍java锁的文章
简单了解下Binlog
基本思路:动态规划,每个格子依次计算,计算当前格子的最小路径和,因为每次移动必定是往下或者往右,因此每个格子的路径和必定来自于上边格子或者左边格子的数字加上当前格子的数字
时间复杂度分析:O(mn),会遍历所有格子,因此复杂度是nm
1 | /** |
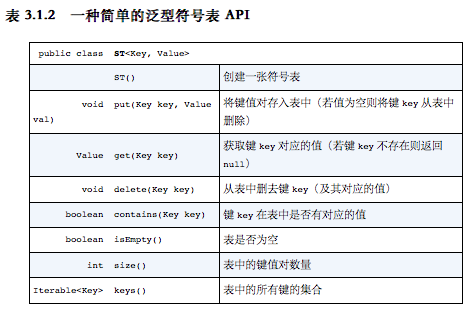
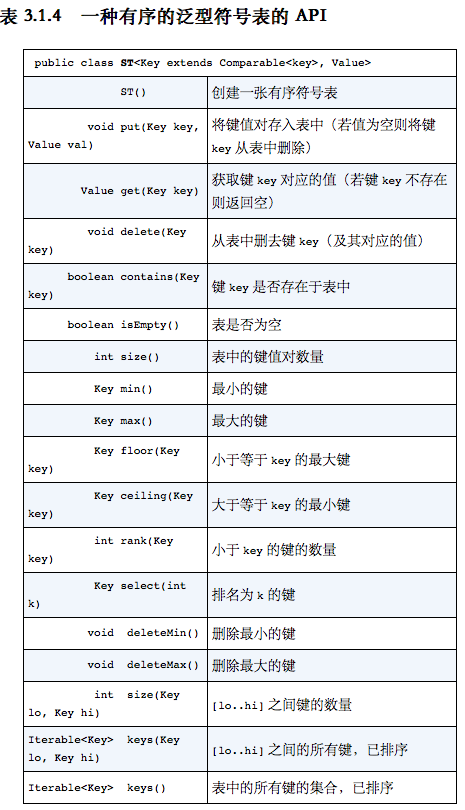







配套网站:https://algs4.cs.princeton.edu/home/