读书笔记-数据结构和算法图解

第一章 数据结构为何重要

• 操作的速度，并不按时间计算，而是按步数计算。理解这个观点，因为不同机器其实运行速度都会有差异，真正决定效率的是一个操作的步数。
• 读取是一步到位，意味着是读取数组的索引
  • 计算机的内存可以看成一堆格子，内存的格子是地址连续的
  • 声明数组时，是在内存中划分出一些连续的格子
  • 查找任意索引，最多都是只需要1步
• 查找意味着从数组中寻找是否存在某个值
  • 计算机需要从索引0开始寻找，即线性查找
  • 查找任意内容，最多步骤为数组的索引长度N
• 计算机知道数组的索引开始位置和结束位置
  • 插入末尾只需要一步，直接在末尾插入即可
  • 开头或中间的位置，需要先移动其他元素的位置，再进行插入
  • 最复杂的插入，是在数组开头插入，意味着需要将N个元素都右移，再将元素插入，即N+1步
• 删除任意元素都需要将右边的元素左移，以保持数组的连续性和完整性
• 最复杂的删除是删除开头元素，删除为1步，之后将N-1个元素左移，最终为N步
• 集合是一种不允许元素重复的数据结构
  • 读取，查找，删除和数组的效率是一致的
  • 插入的效率和数组不同
    • 需要先确定这个元素在不在集合内，因此需要先查找一遍，如前文所诉，最多需要N步
    • 确定要插入的元素不在集合内后，进行插入，和数组一样，最多需要N+1步
    • 因此集合的插入最终的复杂度为2N+1步

第二章 算法为何重要

• 和数组的区别就在于里面的元素是按照规则排序的。读取和删除跟数组效率一样。
• 插入元素
  • 首先需要根据排序规则，从索引0的位置开始遍历，找到这个元素在有序数组中的位置，最多N步
  • 将该位置的元素右移，然后插入，这是2步，因此最多N+2步。
• 查找元素
  • 有序数组的查找比数组的查找效率更高，因为排列有序，所以如果某个元素比查找元素要大，那就可以停止查找。
• 二分查找的前提是有序数组
• 数组长度每次翻倍，二分查找的操作步数只会+1。而线性查找却会跟着一起翻倍。

第三章 大O记法

• 无论数组多大，操作都只要一步，记为O(1)
• 数组长度为N，操作需要用N步，记为O(N)
• 当数据增长时，步数如何变化？
  • O(N) 被称为线性时间，随着数组长度增长，步数每次+1
  • O(1) 被称为常数时间，表示随着数组长度增长，步数不变
• 线性查找的最好情况是O(1)，最坏情况是O(N)。
• 二分查找的复杂度记为O(log N)

第四章 利用大O给代码提速

• 冒泡排序

  • 基本步骤
    • 指针首先指向头两个元素，比较大小，如果左边大于右边，则交换位置
    • 将指针右移一位，重复第一步
    • 到列表末尾，重新到列表头部重复第一二步
    • 直到顺序正确，退出循环
  • 按照最复杂的情况看，也就是完全倒序的列表进行冒泡排序的话，复杂度为O(N^2)

    public static void bubbleSort(int[] nums) {
        for (int i = 0; i < nums.length - 1; i++) {
            for (int j = nums.length - 1; j > i; j--) {
                if (nums[j] < nums[j-1]) {
                    int temp = nums[j];
                    nums[j] = nums[j-1];
                    nums[j-1] = temp;
                }
            }
        }
    }

• 二次问题

  • 解决一个数组中是否存在重复元素的问题
  • 时间复杂度为O(N^2)的解决办法：

    function hasDuplicateValue(array) {
        for(vari=0;i<array.length;i++) {
            for(varj=0;j<array.length;j++){
                if(i!==j&&array[i]==array[j]){
                    return true}
            }
        }
        return false
    }

  • 时间复杂度为O(N)的解决办法：

    function hasDuplicateValue(array) {
        var existingNumbers=[];
        for(vari=0;i<array.length;i++){
            // 将元素成员作为下标
            if(existingNumbers[array[i]]===undefined){
                existingNumbers[array[i]]=1;
            } else {
                returntrue;
            } 
        }
        return false;
    }

第五章 用或不用大O来优化代码

• 选择排序
  • 基本步骤
    • 从索引0开始，遍历数组，找到最小的数，将其和索引0的数字调换位置
    • 第二次循环从索引1开始，找到最小数，和索引1的数字调换位置
    • 如此循环，到最后一个数时就完成了排序
  • 和冒泡排序一样，时间复杂度都表示为O(N^2)，但是实际效率比冒泡排序快一倍，也就是虽然更高效，但是没有指数上的差别
  • 从这个角度说，性能调优不应该盲目只看大O记法所表示的复杂度，如果不能有数量级的差别，也应该具体分析后进行同一数量级的调优

    public static void selectionSort(int[] nums) {
        int minIndex = 0;
        for (int i = 0; i < nums.length - 1; i++) {
            for (int j = i + 1; j < nums.length; j++) {
                if (nums[minIndex] > nums[j]) {
                    minIndex = j; // 获取最小的数
                }
            }
            int temp = nums[i];
            nums[i] = nums[minIndex];
            nums[minIndex] = temp;
        }
    }

第六章 乐观地调优

• 假设排序数组并不是按照最差的情况进行排序，则总是会有更好更高效的方式进行排序
• 插入排序
  • 基本步骤
    • 从索引1开始，将索引1的数字取出作为一个对比数字，然后从索引0开始，直到索引1结束，比较数字和对比数字的大小
    • 遇到比它大的往右移动一位，遇到比它小的数字，或者索引左边的所有数字都右移了就停止这次循环
    • 从索引2开始，重复1，2步骤

def insertion_sort(array):
    for index in range(1,len(array)):
        position = index
        temp_value = array[index]
        while position > 0 and array[position-1] > temp_value:
            array[position] = array[position-1]
            position = position - 1 
        array[position] = temp_value

• 实际时间复杂度为O(N^2 + 2N - 2)，忽略常数和只看最高次的N，则还是O(N^2)
• 看似时间复杂度一样，但是在平均情况下，插入排序的效率是更高的

第七章 查找迅速的散列表

• 散列表即map，或称字典，映射，关联数组
• 查找效率为O(1)
• 简单原理：暂且把散列中的键值对应关系视为乘法关系，如BAD值，转为字母表中的214，对应键为8
• 散列值计算过程（简化）
  • 散列表可以看成是一行能够存储数据的格子，就像数组那样。每个格子都有对应的编号
  • 函数对键进行计算，如BAD=214=8
  • 将BAD存到第8个格子上
  • 当需要查找BAD对应的值时，计算机计算键BAD的散列值=8，因此直接找到第8个位置的值，复杂度为O(1)
• 冲突解决
  • 如上所诉的过程，如果又要存储DAB的值，算出来的散列值也是8，也要存到同一个位置上
  • 将8的位置换成一个数组，即8这个位置可以存储多个键值对
  • DAB的查找过程就变成，先计算散列值为8，然后找到8这个位置的数组，再用线性查找遍历数组，找到DAB
  • 为了减少冲突，散列表的设计需要减少这种冲突，因此实际设计中散列值的计算要复杂很多
• 散列表的效率决定因素
  • 要存多少数据
  • 有多少可用的格子
  • 用什么样的散列函数
  • 要避免冲突，就要增加存储空间，需要找到平衡

第八章 用栈和队列来构造灵巧的代码

• 栈 LIFO（lastin，firstout）后进先出。
  • 只在末尾插入数据
  • 只能读取末尾数据
  • 只能一处末尾数据
  • 栈的末尾叫栈顶，栈的开头成为栈尾
  • 往栈里插入数据，称为压栈
  • 从栈顶移出数据，称为出栈
  • 一般来说，栈都是用来实现某些特殊算法（当数据的处理顺序要与接收顺序相反时），而不会用于存储数据
• 队列 先进先出
  • 只能在末尾插入数据（这跟栈一样）
  • 只能读取开头的数据（这跟栈相反）
  • 只能移除开头的数据（这也跟栈相反）
  • 可用于处理网络数据接收处理等任务

第九章 递归

• 递归必需设置基准情形，即结束递归的条件
• 计算机是用栈来记录每个调用中的函数。这个栈就叫作调用栈，也就是在递归场景中，按照321顺序调用，123顺序完成
• 递归十分适用于那些无法预估计算深度的问题

第十章 飞快的递归算法

• 快速排序
  • 基本步骤
    • 首先找一个基准数，比如找最右边的数
    • 两个指针分别指向数组开头和结尾（排除基准数之外）
    • 两个指针每次都向中间各移动一步，左指针遇到大于等于基准数的数值时就停止移动，右指针遇到小于等于基准数的数值时停止移动
    • 两指针所在数值的位置互换
    • 重复2-4步骤，直到两个指针重合
    • 将基准数与左指针指向的数值互换
  • 以上步骤是以基准数为中心，将数组分为比基准数大的分区和比基准数小的分区，并没有完成最终排序
  • 结合递归，在每个分区内再分别进行快速排序，最终就可以完成排序
  • 可以近似看作长度为N的数组，要进行N个分区的二分查找，二分查找的效率为logN，所以快速排序的效率近似为O(NlogN)
  • 大部分情况下都是表现最好的排序方式，因此多数语言内置排序都以快速排序实现

    public static void quickSort(int a[], int left, int right) {
        int i, j, t, temp;
        if (left > right)
            return;
    
        temp = a[left]; // temp中存的就是基准数
        i = left;
        j = right;
        while (i != j) {
            // 顺序很重要，要先从右边开始找
            while (a[j] >= temp && i < j)
                j--;
            // 再找左边的
            while (a[i] <= temp && i < j)
                i++;
            // 交换两个数在数组中的位置
            if (i < j) {
                t = a[i];
                a[i] = a[j];
                a[j] = t;
            }
        }
        // 最终将基准数归位
        a[left] = a[i];
        a[i] = temp;
    
        quickSort(a, left, i - 1);// 继续处理左边的，这里是一个递归的过程
        quickSort(a, i + 1, right);// 继续处理右边的 ，这里是一个递归的过程
    }

• 快速选择
  • 用于查找无序数组中指定大小的数字，比如长度为10的数组中查找第二小的数字
  • 结合快速排序和二分法，先用快速排序对数组进行分区，每次分完区之后，基准数落下的位置就是这个数组中第几大的数字
  • 根据这个方法，快速选择可以用O(N)的复杂度获取到需要的数字

第十一章 基于结点的数据结构

• 链表
  • 和数组不同的是，链表中的各个元素不是连续的，这种不相邻的格子叫做结点
  • 每个结点存储数据以及下一个结点的地址来实现链表，这些存储下个结点地址的额外数据就是链
  • 链表的好处是不需要内存分配连续的空间
  • 读取
    • 不像连续数组，计算机不知道某个结点的地址，只知道开头结点的地址，因此需要遍历
    • 读取的复杂度为O(N)
  • 查找：读取一样，需要从链表开头进行逐一遍历，复杂度为O(N)
  • 插入
    • 链表的插入需要先找到插入的位置，如前所述，这个过程的时间复杂度为O(N)
    • 随后将插入位置的上一个结点指向的地址改为当前结点的地址，复杂度为O(1)
    • 和有序列表相反的是，在表头插入数据步骤是最少的，在最后一位插入步骤是最多的
  • 删除：大致上和插入的原理差不多，时间复杂度同样为O(N)
• 为什么用链表
  • 从上述分析看，链表增删改查的效率并没有比数组快
  • 但在某些业务场景下，比如从一堆数组中删除指定条件的无效数据
    • 数组的操作过程是，每次找到一条无效数据后，先进行删除，然后将右边的数据进行左移，如果在最坏的情况下，无效数据都在数组开头，那每次删除都相当于要移动一遍整个数组
    • 链表的操作过程，省略了每次删除后左移的过程，只需遍历一次数组即可
    • 增加数据也是同理
  • 因此，相比数组，链表的增删效率更高
• 双向链表
  • 即每个结点除了存储下个结点的地址，还会存储上一个结点的地址
  • 增删改查可以从头部或者尾部开始
  • 这种特性可以使双向链表作为队列的底层实现，这样增删复杂度都是O(1)

第十二章 二叉树

• 前文提到，有序列表的查找(二分法 O(logN))和读取 (O(1))非常快，但是插入和删除效率较低(O(N))；而散列表的查找，插入和删除效率较高(O(1))，但却是无序的
  
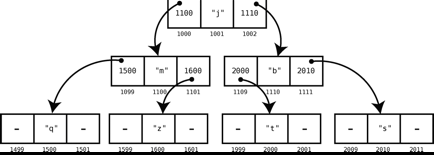
• 二叉树
  • 每个结点链接着另外两个结点
  • 最上面的那一结点（此例中的“j”）被称为根
  • 此例中，“j”是“m”和“b”的父结点，反过来，“m”和“b”是“j”的子结点。“m”又是“q”和“z”的父结点，“q”和“z”是“m”的子结点
  • 树可以分层。此例中的树有3层
  • 每个结点的子结点数量可为0、1、2
  • 如果有两个子结点，则其中一个子结点的值必须小于父结点，另一个子结点的值必须大于父结点
• 二叉树查找的原理类似于二分法，因此复杂度为O(logN)
• 插入同样也是O(logN)，因为找到需要插入的结点即可，无需像有序数组那样移动
• 需要乱序生成的二叉树才能高效，原理看图可知
  
  
• 二叉树的删除
  • 规则较多，如果是删除最底下的子结点复杂度为O(logN)，但是如果删除某个父结点，需要考虑
  • 如果要删除的结点有一个子结点，那删掉它之后，还要将子结点填到被删除结点的位置上
  • 如果要删除的结点有两个子结点，则从其子结点中选取后继结点。后继结点的选取规则是，所有比被删除结点大的子结点中，最小的那个。下图例子中就是将61作为替换
    
    
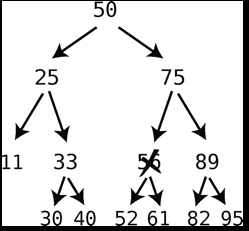
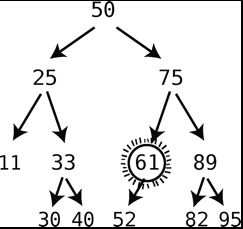
  • 查找后继结点的方法：跳到被删除结点的右子结点，然后一路只往左子结点上跳，直到没有左子结点为止，则所停留的结点就是被删除节点的后继结
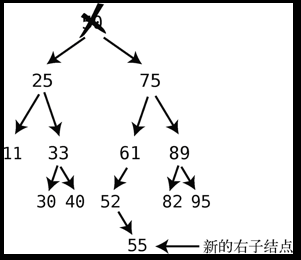
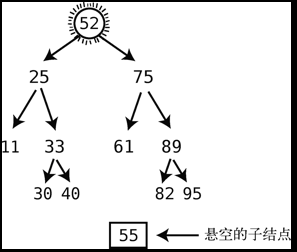
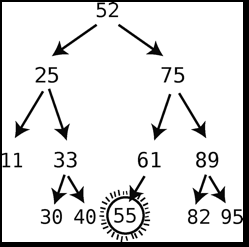
    • 如果后继结点带有右子结点，则在后继结点填补被删除结点以后，用此右子结点替代后继结点的父节点的左子结点
      
      
      
  • 尽管看起来规则复杂，然而这些额外步骤都是寥寥几步就可以完成，删除的主要过程依然是查找结点的过程，所以复杂度还是O(logN)

第十三章 连接万物的图

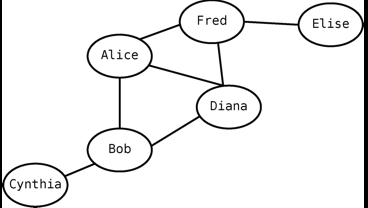
• 每个结点都是一个顶点，每条线段都是一条边。当两个顶点通过一条边联系在一起时，我们会说这两个顶点是相邻的。
• 以Facebook和twitter为例，facebook是双向的关系，而twitter是单向的
  
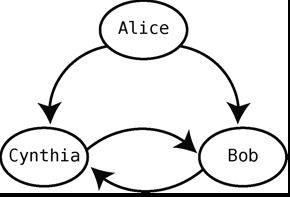
• 可用散列表来实现图
• 广度优先搜索
  • 需要用队列记录后续要处理哪些顶点
  • 找出当前顶点的所有邻接点。如果有哪个是没访问过的，就把它标为“已访问”，并且将它入队。（尽管该顶点并未作为“当前顶点”被访问过。）
  • 如果当前顶点没有未访问的邻接点，且队列不为空，那就再从队列中移出一个顶点作为当前顶点。
  • 如果当前顶点没有未访问的邻接点，且队列里也没有其他顶点，那么算法完成。
  • 简单点说就是每次只处理下一层的数据